Significado de Ascendente y Descendente en Matemáticas

Las secuencias ascendentes y descendentes son conceptos fundamentales en matemáticas que nos ayudan a entender el orden y la progresión de los números. Estas secuencias son especialmente útiles a la hora de identificar patrones, resolver problemas lógicos y analizar fenómenos de crecimiento o disminución progresiva.

En este artículo, exploraremos en detalle qué significa ascendente y descendente en el contexto de las matemáticas, proporcionaremos ejemplos concretos para ilustrar estos conceptos y discutiremos la importancia de comprenderlos en nuestras vidas cotidianas.

Definición de ascendente y descendente en matemáticas

En matemáticas, una secuencia ascendente es aquella en la que cada término es mayor que su término anterior. Esto significa que los números en la secuencia van incrementando en valor a medida que avanzamos.

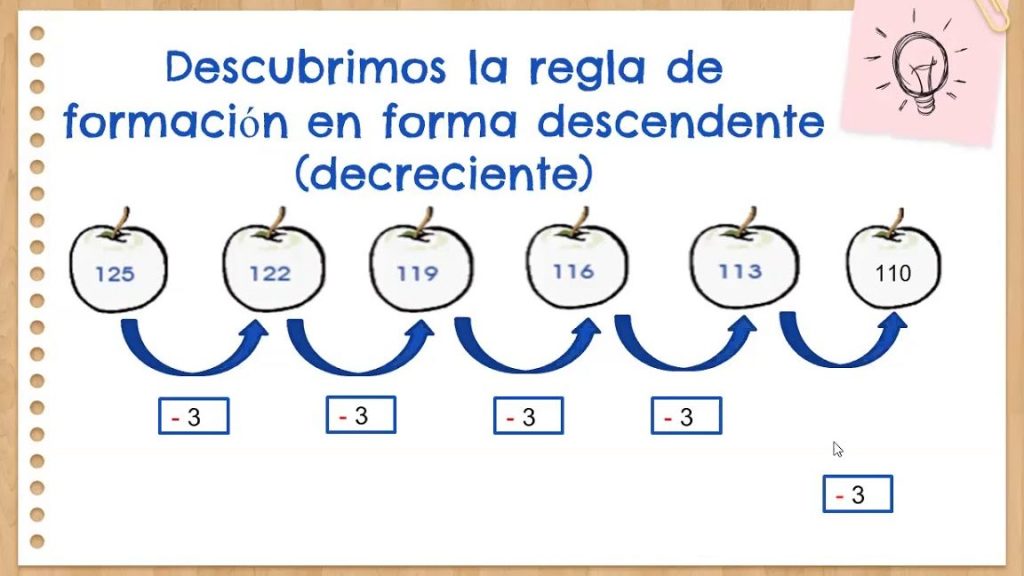
Por otro lado, una secuencia descendente es aquella en la que cada término es menor que su término anterior. Esto implica que los números en la secuencia van disminuyendo en valor a medida que avanzamos.

Ambas secuencias, ascendente y descendente, siguen un patrón particular que las distingue del resto de secuencias. La clave para identificar una secuencia ascendente o descendente es comparar cada término con el anterior y observar si está aumentando o disminuyendo.

Una secuencia ascendente es aquella en la que cada término es mayor que su término anterior, mientras que una secuencia descendente es aquella en la que cada término es menor que su término anterior.

Ejemplos de secuencias ascendentes y descendentes

Para comprender mejor estos conceptos, veamos algunos ejemplos concretos de secuencias ascendentes y descendentes:

1. Secuencia ascendente de números naturales:
1, 2, 3, 4, 5, 6, ...

En esta secuencia, cada término es mayor que el anterior, ya que cada número natural consecutivo es mayor que el anterior. Por lo tanto, esta secuencia es una secuencia ascendente.

2. Secuencia descendente de números pares:
10, 8, 6, 4, 2, 0, ...

En esta secuencia, cada término es menor que el anterior, ya que cada número par consecutivo es menor que el anterior. Por lo tanto, esta secuencia es una secuencia descendente.

3. Secuencia ascendente de potencias de 2:
1, 2, 4, 8, 16, 32, ...

En esta secuencia, cada término es mayor que el anterior, ya que cada potencia de 2 consecutiva es mayor que la anterior. Por lo tanto, esta secuencia es una secuencia ascendente.

4. Secuencia descendente de números impares:
99, 97, 95, 93, 91, ...

En esta secuencia, cada término es menor que el anterior, ya que cada número impar consecutivo es menor que el anterior. Por lo tanto, esta secuencia es una secuencia descendente.

Estos ejemplos ilustran cómo las secuencias ascendentes y descendentes pueden presentarse en diferentes contextos matemáticos y cómo podemos identificarlas mediante la comparación de términos consecutivos.

Aplicaciones de las secuencias ascendentes y descendentes en la vida cotidiana

Si bien las secuencias ascendentes y descendentes son conceptos matemáticos, su aplicabilidad trasciende el ámbito académico y se extiende a nuestra vida cotidiana. Estas secuencias pueden ayudarnos a reconocer patrones, tomar decisiones informadas y resolver problemas numéricos.

Un ejemplo claro de aplicación de estas secuencias en la vida cotidiana es la programación informática. En la programación, las secuencias ascendentes y descendentes se utilizan para iterar sobre una serie de instrucciones y realizar tareas repetitivas. El uso de secuencias ascendentes o descendentes en la programación permite automatizar procesos y resolver problemas de manera eficiente.

Otra aplicación de las secuencias ascendentes y descendentes se encuentra en las finanzas personales. Al seguir una secuencia ascendente o descendente de números, podemos analizar el crecimiento o la disminución de nuestros ingresos, gastos o inversiones a lo largo del tiempo. Esto nos permite tomar decisiones informadas sobre cómo administrar nuestro dinero y planificar nuestro futuro financiero.

Además, las secuencias ascendentes y descendentes también son útiles en la resolución de problemas en ciencias naturales y sociales. Por ejemplo, en la física, se utilizan secuencias ascendentes o descendentes para modelar el movimiento de objetos o el cambio de variables en experimentos. En la sociología, las secuencias ascendentes y descendentes se aplican para analizar el cambio de comportamiento en poblaciones y entender cómo se propagan las influencias sociales.

Las secuencias ascendentes y descendentes tienen aplicaciones prácticas en la vida cotidiana, desde la programación informática hasta las finanzas personales y las ciencias naturales y sociales. Comprender estos conceptos matemáticos nos permite tomar decisiones más informadas, resolver problemas numéricos y comprender mejor los patrones que nos rodean.

Conclusiones y reflexiones sobre la importancia de comprender estos conceptos en matemáticas

Las secuencias ascendentes y descendentes son conceptos matemáticos fundamentales que nos permiten comprender el orden y la progresión de los números. Estas secuencias son esenciales en el análisis de patrones, la resolución de problemas y la toma de decisiones informadas en diversos contextos.

Mediante el estudio de ejemplos concretos, como la secuencia ascendente de números naturales o la secuencia descendente de potencias de 2, podemos identificar las características distintivas de las secuencias ascendentes y descendentes. Estas características nos permiten reconocer patrones y establecer lógicas que nos ayudan a resolver problemas de manera más eficiente.

Además, comprender las secuencias ascendentes y descendentes es crucial en nuestras vidas cotidianas. Estas secuencias se aplican en campos tan diversos como la programación informática, las finanzas personales, las ciencias naturales y sociales, entre otros. Conocer cómo funcionan estas secuencias nos permite tomar decisiones informadas, resolver problemas numéricos y comprender mejor el mundo que nos rodea.

Las secuencias ascendentes y descendentes son conceptos matemáticos fundamentales con una amplia aplicación práctica. Al comprender y aplicar estos conceptos, podemos desarrollar habilidades de análisis, resolución de problemas y toma de decisiones que son esenciales tanto en el ámbito académico como en la vida cotidiana. Por lo tanto, es importante dedicar tiempo y esfuerzo a comprender y practicar estos conceptos para fortalecer nuestra comprensión de las matemáticas y mejorar nuestras habilidades en diferentes áreas de la vida.